编译原理笔记
编译原理求语法树直接短语等等
短语
对所有非叶节点进行前序遍历
直接短语
父节点只有一个节点的叶节点
句柄
直接短语中最左边的
素短语
至少含有一个终结符且不含其他更小的素短语
终结符:小写字母或者符号

消除左递归 消除回溯
消除左递归
\begin{aligned}\text{形式:} & A\to A\alpha|\beta \\\text{改为:} & \begin{cases}A\to\beta A^{\prime} \\A^{\prime}\to\alpha A^{\prime}|\varepsilon & \end{cases}\end{aligned}
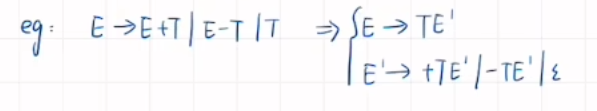
消除回溯
\begin{aligned}& \text{形式:}A\to\delta\beta_1|\delta\beta_2|\cdots|\delta\beta_i|\beta_{i+1}|\cdots|\beta_j \\& \text{改为:}\begin{cases}A\to\delta A^{\prime}|\beta_{i+1}|\beta_j \\A^{\prime}\to\beta_1|\cdots|B_i & \end{cases}\end{aligned}
求first集和follow集
first集
看产生式的左边,产生的符号如果是终结符,则加入first集,如果是非终结符,则将该非终结符的first集放入所求的fitst集
follow集
- 文法开始符的follow集需要加\#
- 若A\to \alpha B,B后面为空,则将follow(A)加入follow(B)
- 若A\to\alpha B\beta,则将\beta加入follow(B)
- 若A\to\alpha BC,则将first(C)加入follow(B)

构造LL(1)文法
-
消除左递归,消除回溯
-
求first集和follow集
-
判断是否符号LL(1)文法
对于一个产生式,如果A\to \alpha|\beta \begin{cases} first\{\alpha\}\cap first\{\beta\} = \empty , \alpha \beta \text{均不是空串}\\ first\{\alpha\}\cap follow\{A\} = \empty , \alpha \text{不是空串,}\beta\text{是空串} \end{cases},则是LL(1)文法
-
构造分析表
-
非递归预测分析法:
初始时符号栈为
$A,(左边为栈底,右边为栈顶)。如果栈顶是非终结符,则将输入串的首位(当前输入符号)与分析表对比进行化简,如果栈顶的符号是终结符且与当前输入符号相同,则消去该终结符。不断重复直输入串为空,分析成功。
已知文法G[S]为:
S \to aTUb ∣ε
T \to cUc∣bUb ∣aUa
U \to Sb ∣cc
(1)写出各非终结符的FIRST集和FOLLOW集。(5分)
(2)构建LL(1)分析表, 本文法是LL(1)文法吗,为什么? (10分)
(3)如果是LL(1)文法,基于分析表,试给出aababb的分析过程。(5分)

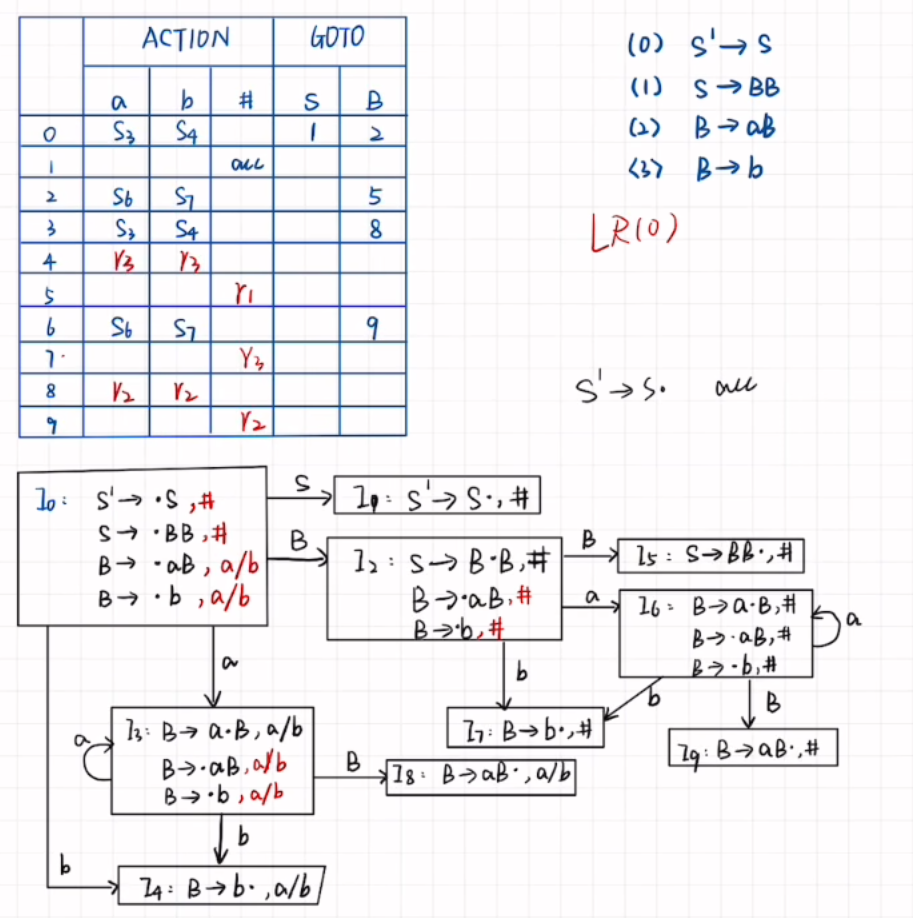
构造LR(0)分析表
分析LR(0)自动机
-
写成增广文法
如果G是一个以S为开始符号的文法,则G的增广文法G'就是在G中加上新开始符号S′和产生式S'\toS而得到的文法。如图,添加文法(0)后变为增广文法

-
LR(0)项:
一个LR(0)项是一个产生式A \to \alpha \cdot \beta,其中点号
·表示在产生式右部的某个位置。- 如果点号在最左边,表示我们期望看到\alpha \beta。
- 如果点号在最中间,表示我们已经匹配了\alpha,现在期望匹配\beta。
- 如果点号在最右边,表示我们已经匹配了整个产生式\alpha \beta,可以进行归约。
-
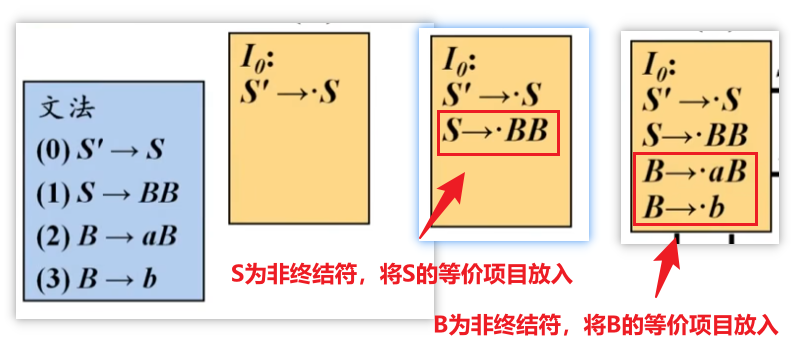
给定一个LR(0)项集I,它的闭包Closure(I)定义如下:
- 初始: 将I中的所有项添加到Closure(I)。
- 迭代: 如果A \to \alpha \cdot B \beta是一个在Closure(I)中的项,并且B是非终结符,那么对于B的所有产生式B \to \gamma,将项B \to \cdot \gamma添加到Closure(I)。重复此过程直到没有新的项可以添加。
直观理解: 当我们看到一个项A \to \alpha \cdot B \beta时,这意味着我们希望接下来匹配非终结符B。为了匹配B,我们必须开始匹配B的某个产生式的右部。因此,我们需要将所有B的产生式B \to \gamma的初始项B \to \cdot \gamma加入到当前的项集中,以表示我们现在可以开始识别这些产生式的右部。
-
GoTo 操作
GoTo操作定义了LR(0)DFA的状态转移。给定一个LR(0)项集I和一个文法符号X(终结符或非终结符),GoTo(I, X)定义如下:
- 找到I中所有形如A \to \alpha \cdot X \beta的项。
- 对于这些项,将点号向右移动一位,得到A \to \alpha X \cdot \beta。
- 对这些新项组成的集合求闭包。
直观理解: 如果当前状态是I,并且我们看到了符号X,那么我们已经成功匹配了X。因此,所有点号前面是X的项,其点号都应该向右移动一位,表示X已经被识别。然后,我们需要对这些新项的集合求闭包,以考虑可能由新项引起的新的识别期望。
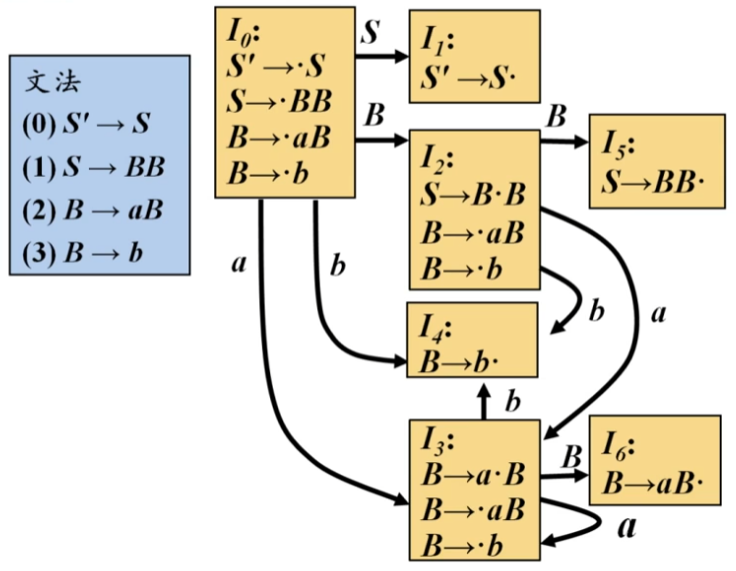
如图,在状态I_0,如果下一个符号是S,则进入状态I_1,如果下一个符号是B,则进入状态I_2,同时对每个状态都要重复步骤3的闭包操作
构造LR(0)分析表
分析表有三列,分别为"状态","action","goto"
action:底下是所有终结符(包括结束符\$)
goto:底下是所有非终结符
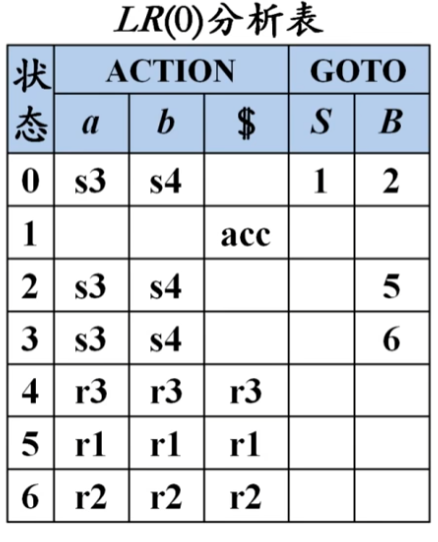
接下来进行分析表构建:
- 对于状态0(I_0),下一个符号为终结符
a时进入状态I_3,记为s3,下一个符号为终结符b时进入状态I_4,记为s4。 - 对于状态0(I_0),下一个符号为非终结符
S时进入状态I_1,记为1,下一个符号为B时进入状态I_2,记为2。 - 对于状态1(I_1),遇到结束符\$时完成接收,记为
acc - 对于状态4(I_4),状态4是规约状态,不管遇到什么符号都会进行规约,对应[第三条产生式B\to b](#Production Rules)
- 其他状态同理
SLR
首先构造LR(0)分析表,但是不进行规约(分析表构建的第四步)。
接下来求构造文法的follow集,只有follow集中的元素才进行规约(在分析表中写r)

如果还有冲突,则需要使用LR1分析法
LR(1)
步骤:
- 增广文法
- 构造方法与LR(0)类似,但是需要在每个产生式后面写展望符,对于同一个产生式,展望符不同,那么这两个就不一样
- 在第一个产生式的后面写展望符\$
- 在进行闭包操作时,如果A\to\alpha\cdot B,x,B后面是空串,x表示某个展望符,则B\to\cdot \alpha的展望符是x。
如果A\to\alpha\cdot BC,x,B后面是非终结符C,则B\to\cdot \alpha的展望符是C的first集。
如果A\to\alpha\cdot B\beta,x,B后面是终结符\beta,则B\to\cdot \alpha的展望符是\beta。 - 在进行规约状态时,只有遇到展望符才会规约(对比LR(0):所有都规约,SLR:follow集才规约)
LALR(1)
如果除展望符外,两个LR(1)项目集是相同的,则称这两个LR(1)项目集是同心的
步骤:
- 求LR(1)
- 合并同心项目集
已知文法G[S]为:
S\toAa|bAc|dc|bda
A\tod
(1)构造该文法的SLR(1)语法分析表。(10分)
(2)该文法否为SLR(1)文法,说明理由。(2分)
(3)构造该文法的LALR(1)分析表,该文法是否为LALR(1)文法,说明理由。(8分)
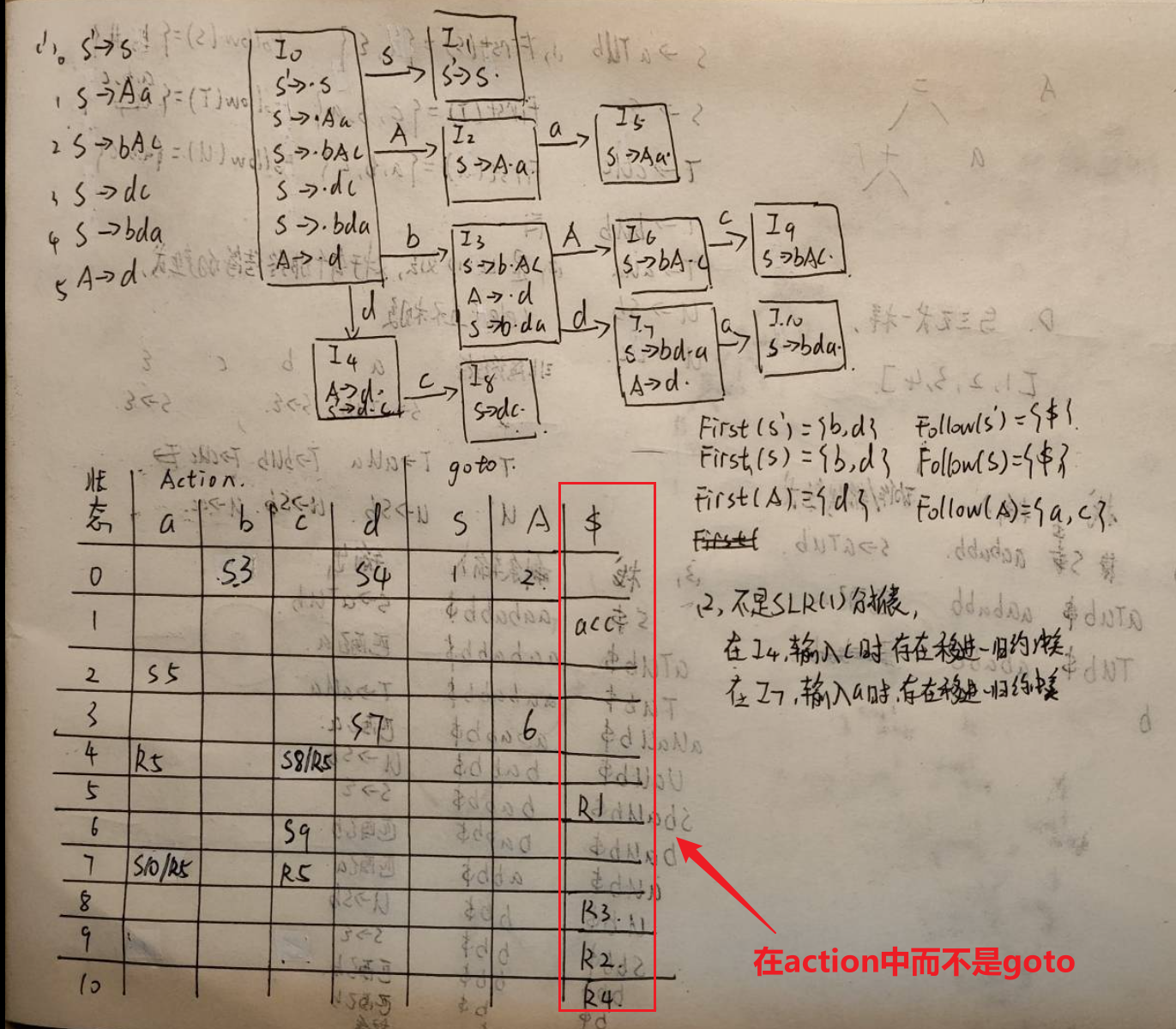
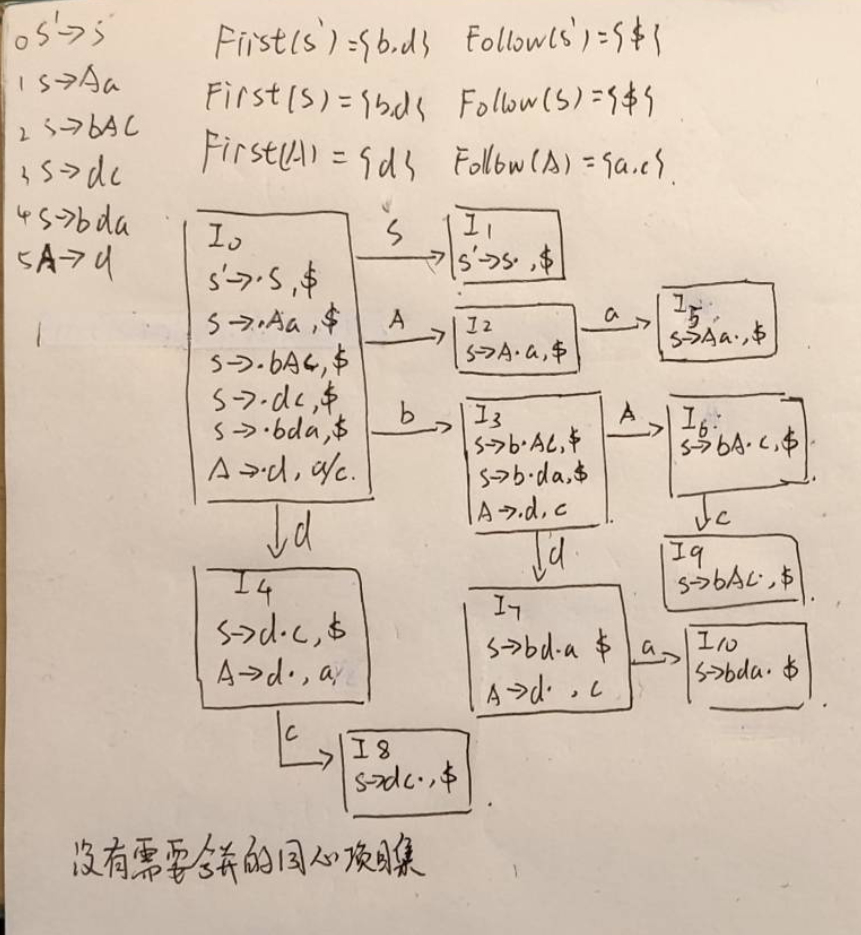
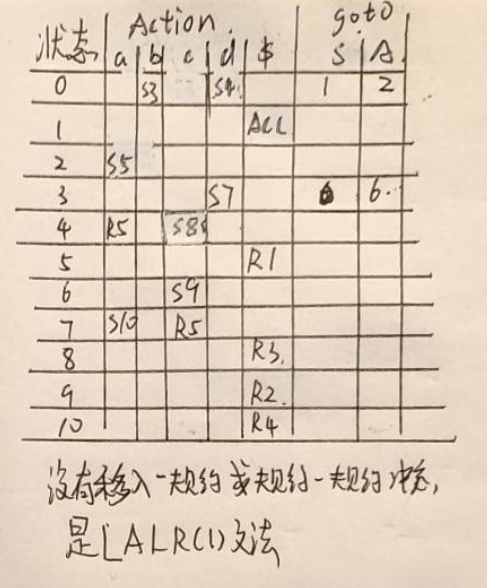
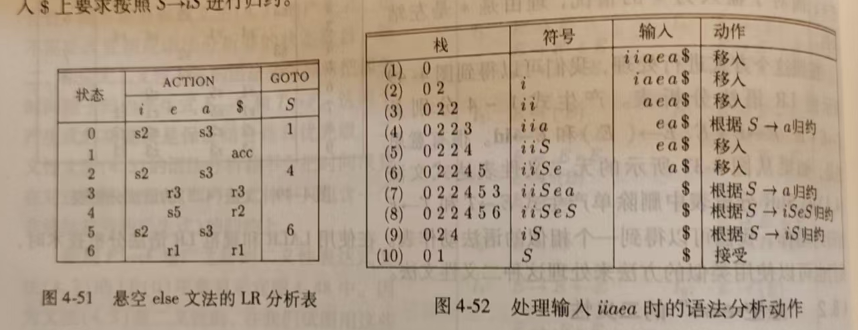
LR(0)、SLR、LR(1)、LALR(1)的分析过程见下图
四元式
(ai生成)
四元式是编译器中间代码表示的一种形式,由四个组成部分构成,通常用于描述程序中的运算或控制流程。其基本结构为:
(运算符, 操作数1, 操作数2, 结果)
四元式的组成
- 运算符(OP):表示具体的操作(如加减乘除、赋值、跳转等)。
- 操作数1(Arg1):第一个操作数(可以是变量、常量或临时变量)。
- 操作数2(Arg2):第二个操作数(若运算符是单目操作,此项可能为空)。
- 结果(Result):存储运算结果的变量或临时变量。
示例
-
算术运算对于表达式
a = b + c * 2,对应的四元式序列可能为:(*, c, 2, t1) // t1 = c * 2 (+, b, t1, t2) // t2 = b + t1 (=, t2, _, a) // a = t2 -
控制语句
对于if (x > 0) goto L1,四元式为:(j>, x, 0, L1) // 若x>0则跳转到标签L1
三元式
(ai生成)
三元式是编译器中间代码表示的一种形式,由三个部分组成,用于描述程序中的运算或控制流程。其基本结构为:
(运算符, 操作数1, 操作数2)
三元式的组成
- 运算符(OP):表示具体的操作(如算术运算、逻辑运算、跳转等)。
- 操作数1(Arg1):第一个操作数(可以是变量、常量或指向其他三元式的指针)。
- 操作数2(Arg2):第二个操作数(若运算符是单目操作,此项可能为空)。
与四元式的区别:
- 四元式 显式存储运算结果(如
t1 = a + b),而 三元式 通过 位置索引 隐式引用中间结果。 - 三元式更紧凑,但优化和代码生成时可能不如四元式直观。
示例
1. 算术运算
对于表达式 a = b + c * 2,三元式序列如下:
(0) (*, c, 2) // c * 2
(1) (+, b, (0)) // b + (0)的结果
(2) (=, a, (1)) // a = (1)的结果
(0)、(1)等编号代表三元式的位置,用于引用中间结果。
2. 控制语句
对于 if (x > y) goto L1,三元式为:
(j>, x, y)
跳转目标 L1 通常由符号表或额外信息管理。
三元式的特点
- 节省空间:相比四元式,不显式存储临时变量,减少存储开销。
- 依赖位置引用:中间结果通过三元式编号引用,可能增加优化复杂度。
- 适合线性结构:便于顺序处理,但嵌套引用(如
(+, b, (0)))可能降低可读性。
三元式 vs 四元式
| 特性 | 三元式 | 四元式 |
|---|---|---|
| 存储方式 | 隐式引用结果(通过编号) | 显式存储结果(临时变量) |
| 可读性 | 嵌套引用较难跟踪 | 更直观,适合调试和优化 |
| 空间效率 | 更高(无临时变量存储) | 略低(需存储结果变量) |
| 优化支持 | 依赖额外信息,优化较复杂 | 直接操作临时变量,优化更方便 |
间接三元式
(ai生成)
间接三元式(Indirect Triples)
间接三元式是三元式的一种优化形式,主要用于解决三元式在代码优化和调整时的引用问题。它在三元式的基础上引入了一个间接引用表(Indirection List),使得中间代码更容易被修改和重组,而不会破坏原有的引用关系。
1. 基本结构
间接三元式由两部分组成:
- 三元式表(Triples Table)存储实际的三元式,格式为
(运算符, 操作数1, 操作数2),其中操作数可以是变量、常量或指向三元式表的索引。 - 间接引用表(Indirection List)
存储三元式的执行顺序,每个条目指向三元式表中的某个三元式。
示例
假设有以下代码:
x = a + b * c;
if (x > 0) goto L1;
(1) 普通三元式表示
(0) (*, b, c) // t1 = b * c
(1) (+, a, (0)) // t2 = a + t1
(2) (=, x, (1)) // x = t2
(3) (j>, x, 0) // if x > 0 goto L1
- 问题:如果优化时删除或移动三元式,所有引用它的位置(如
(1)引用(0))都需要调整,维护成本高。
(2) 间接三元式表示
三元式表(Triples Table):
(0) (*, b, c)
(1) (+, a, (0))
(2) (=, x, (1))
(3) (j>, x, 0)
间接引用表(Execution List):
[0, 1, 2, 3] // 执行顺序:先计算 (0),再 (1),然后 (2),最后 (3)
- 优化时:只需调整间接引用表的顺序,而不修改三元式本身的引用关系。
2. 间接三元式的优势
-
优化友好
- 在代码优化(如删除冗余计算、调整执行顺序)时,只需调整间接引用表,而无需修改三元式内部的引用。
- 例如,如果
(0)的计算结果可被复用,只需在间接引用表中调整其位置,而不会影响其他三元式。
-
便于代码移动
- 在循环优化(如循环不变外提)时,可以轻松调整三元式的执行顺序,而不会破坏依赖关系。
-
调试更清晰
- 间接引用表可以记录优化的历史,便于调试时查看中间代码的变换过程。
3. 间接三元式 vs 普通三元式 vs 四元式
| 特性 | 普通三元式 | 间接三元式 | 四元式 |
|---|---|---|---|
| 存储方式 | (OP, Arg1, Arg2) |
(OP, Arg1, Arg2) + 间接表 |
(OP, Arg1, Arg2, Res) |
| 引用方式 | 直接引用三元式编号 | 通过间接表引用 | 显式存储临时变量 |
| 优化灵活性 | 低(修改三元式会破坏引用) | 高(仅调整间接表) | 中(依赖临时变量) |
| 适用场景 | 简单代码生成 | 需要优化的中间代码 | 通用型编译器设计 |
4. 适用场景
- 间接三元式 适用于需要频繁优化的编译器前端,特别是在:
- 循环优化(如循环展开、代码外提)
- 公共子表达式消除
- 死代码删除
- 四元式 更适用于现代编译器(如 LLVM IR、GCC RTL),因为它更接近机器码,便于寄存器分配和指令选择。
- 普通三元式 适用于简单编译器或内存受限环境。
5. 总结
-
间接三元式 = 三元式 + 间接引用表,优化时更灵活。
-
解决了普通三元式难以调整执行顺序的问题。
-
适用于需要复杂优化的编译器,但现代编译器更多采用 SSA(静态单赋值) 或 四元式 的变种(如 LLVM IR)。
将算术表达式a=(b+c)*d+c翻译成 A. 抽象语法树 B. 四元式 C. 三元式 D. 间接三元式
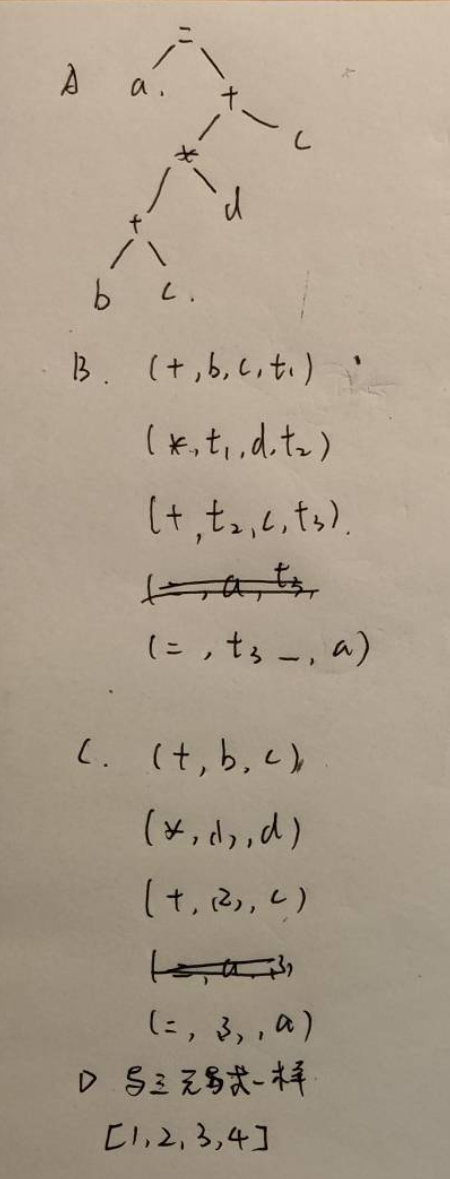
语法制导
综合属性:在分析树结点N上的非终结符A的综合属性只能通过N的子结点或N本身的属性值来定义
继承属性:在分析树结点N上的非终结符A的继承属性只能通过N的父结点、N的兄弟结点或N本身的属性值来定义。(终结符没有继承属性)
向上综合,向下继承
每个节点都带有属性值的分析树称为注释分析树
注释分析树画法查看博客【编译原理】语法制导的语义计算——注释分析树
S属性:仅仅使用综合属性(只与子节点和自身有关)
L属性:L是left的意思,属性与子节点和左兄弟节点有关,不能与右兄弟节点相关
每个S属性都是L属性
类型表达式
赋值语句
主要任务是生成三地址码
x=(a+b)*c
数组
int[5][5]
array(5,array(5,int))
记录(结构体)
record \{char\ x; char\ y;\}p
record((x × char) × (y × char))
正则表达式\toNFA\toDFA
正则表达式语法参考这篇笔记
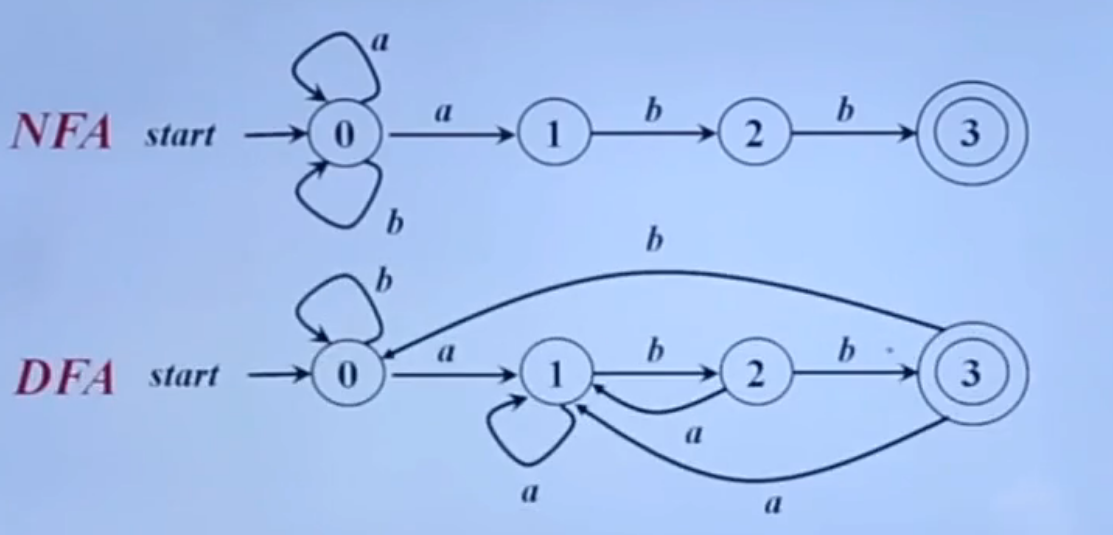
NFA与DFA区别,在DFA中,对于任意一个圈,出去的有向边不能有相同的符号,而NFA可以。
正则表达式\toNFA
-
对于空串\epsilon
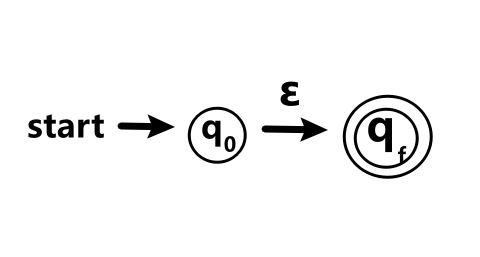
-
对于符号a
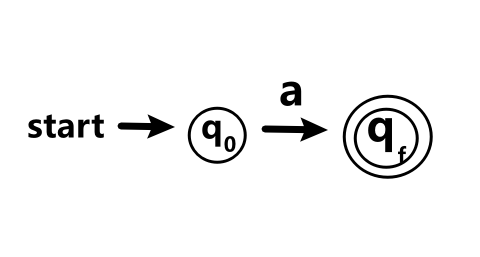
-
对于表达式r=ab
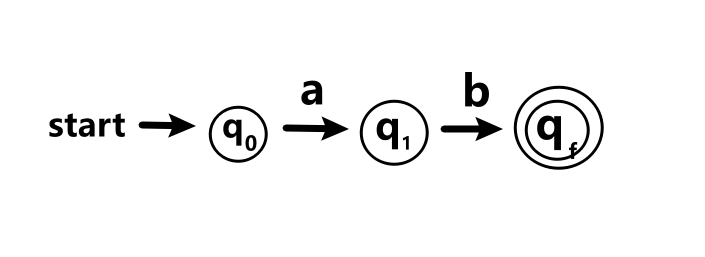
-
对于表达式r=a|b
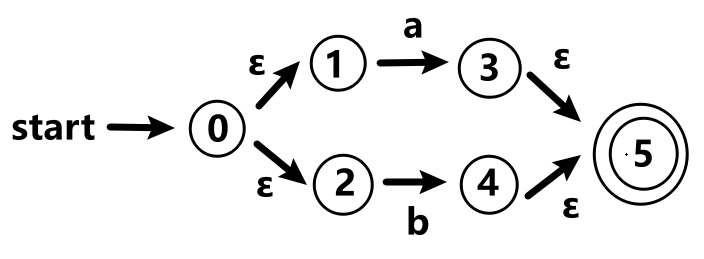
-
对于表达式r=(a)*
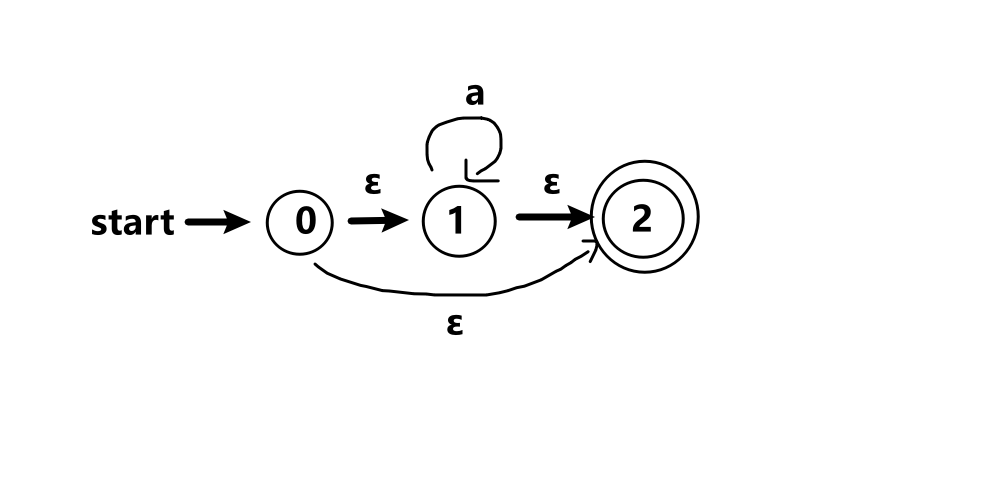
-
对于表达式r=(a|b)^*abb
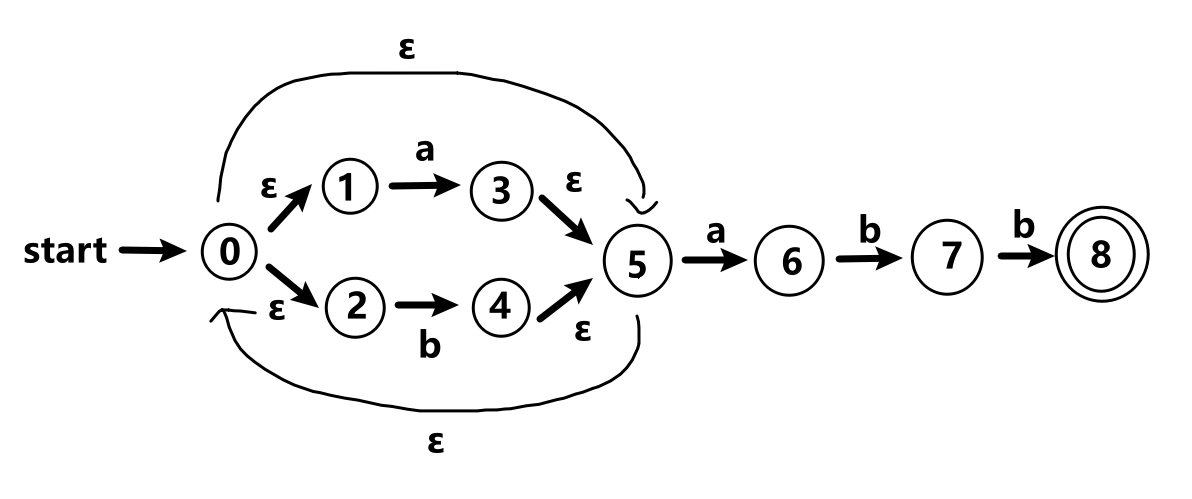
NFA\toDFA
如果某个状态q_a可以通过空字符串到达q_b,则q_a和q_b属于同一个集合,如上图,状态0、1、2、5属于同一个集合。
先写DFAD状态转换表
- 一共有2+n列,2分别是NFA状态、DFA状态,n是出现的字符
- NFA状态是一个集合,DFA状态是大写字母ABC等
- 对于上图,初始NFA状态是{0,1,2,5},DFA状态记为A,可以接收符号a,然后NFA状态变为状态{3,5,0,1,2,6}记为B(1接收a变为3,5接收a变为6);A可以接收符号b变为状态{4,5,0,1,2},记为C
- 状态B接受符号a,变为状态B。接受符号b,变为状态{4,5,0,1,2,7},记为D
- 状态C接收符号a,变为状态B。接受符号b,变为状态C
- 状态D接收符号a,变为状态B。接收符号b,变为状态{4,5,0,1,2,8},记为状态E
- 状态E接收符号a,变为状态B。接收符号b,变为状态C
- 最终完成表格
NFA状态 DFA状态 a b {0,1,2,5} A B C {0,1,2,3,5,6} B B D {0,1,2,4,5} C B C {0,1,2,4,5,7} D B E {0,1,2,4,5,8} E B C
然后根据表格完成DFA
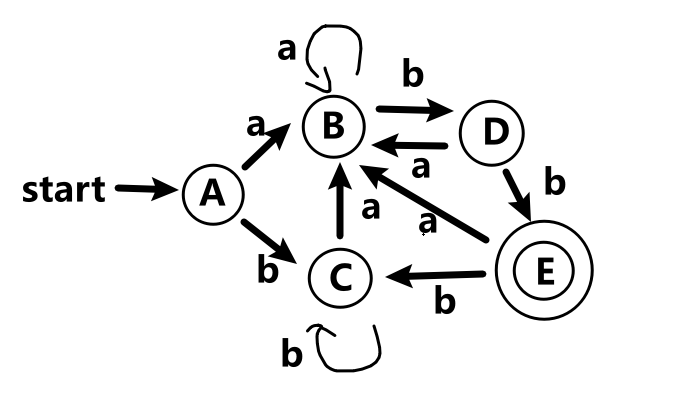
注:如果一个集合中含有最后的状态(如上图的状态8),则都要画两个圈(状态E)
DFA化简
将DFA中的所有状态分为两个集合,终态(E)和非终态(A、B、C、D)
如果一个集合接受了一个元素后会变成另一个集合的元素,则需要将集合拆分
零散的各种小知识点
- 词法分析是编译过程中的第一个阶段,其主要任务是将输入的字符序列(源代码)转换为有意义的词法单元(tokens),例如标识符、关键字、运算符等。这一过程的核心依据是构词规则(即如何将字符组合成合法的单词或符号)
- 移进项目:当点后面是一个终结符时,表示下一步需要将这个终结符移进(shift)到栈中。因此, A \rightarrow \alpha \cdot a \beta 是一个移进项目。
- 归约项目:当点在产生式的最右端时(如 A \rightarrow \alpha \cdot ),表示可以进行归约(reduce)。
- 接受项目:特指当点在增广文法的开始符号的产生式的最右端时(如 S' \rightarrow S \cdot ),表示分析成功。
- 待约项目:当点后面是一个非终结符时(如 A \rightarrow \alpha \cdot B \beta ),表示需要等待进一步规约到 B 。
- 对于一个非二义性的上下文无关文法(CFG),其定义是:每个句子对应唯一的语法树。
- LL(1)文法都不是二义的。
- 乔姆斯基(Chomsky)把文法分成四种类型,即0型、1型、2型和3型。
0型:短语文法(无限制文法)
1型:上下文有关
2型:上下文无关
3型:正则文法
本笔记参考